PID制御より賢く、強化学習より実用的
Smart MPC
Smart MPCとは?
Smart MPC (Model Predictive Control)はモデル予測制御と機械学習を組み合わせた制御アルゴリズムです。 モデル予測制御の長所を引き継ぎつつ、その欠点であるモデリングの難しさを機械学習によるデータドリブンな方法で解決します。
この技術によって、データを取る環境さえ用意することが出来れば、導入コストが高いモデル予測制御を比較的簡単に運用可能になります。
倒立振子を用いた実験
上の動画はSmart MPCによって倒立振子の動きを学習しながら制御している様子です。
実験では適当に設定した様々なパラメータに対して動画同様に数エピソードで学習が収束し、安定して立て続けられるようになっていることがわかりました。
DQN(Deep Q-Network)で同様の実験を行うと、ポールを立てられるようになるまで数百エピソードを必要とする上、一度立てられるようになっても、学習が進むにつれてまた失敗するようになってしまうなど不安定な挙動を示すことがあり、安定した学習には非常に高度なノウハウが要求されます。
また、PID制御ではドリフトが起こりやすく、それを防ぐためには熟練した調整スキルと多くの時間が必要となります。
実験そのものはノートPCのCPUを用いてほぼリアルタイム(1step=0.04秒)で制御を行うことが出来、計算量の軽さといった面からも非常に実用的であるということがわかりました。
このような扱いやすい性質から、Smart MPCはプラントの制御などの問題に対して実用性の高いアルゴリズムであると考えています。
ロボットアームの制御
動画内ではロボットアームの制御をSmart MPCによって行っています。スタート地点(黄色いボール)から出発し、ゴール地点(白いボール)まで指先を移動させるという動作を数エピソードで学習し、安定して制御出来ている様子が分かります。
アーキテクチャ
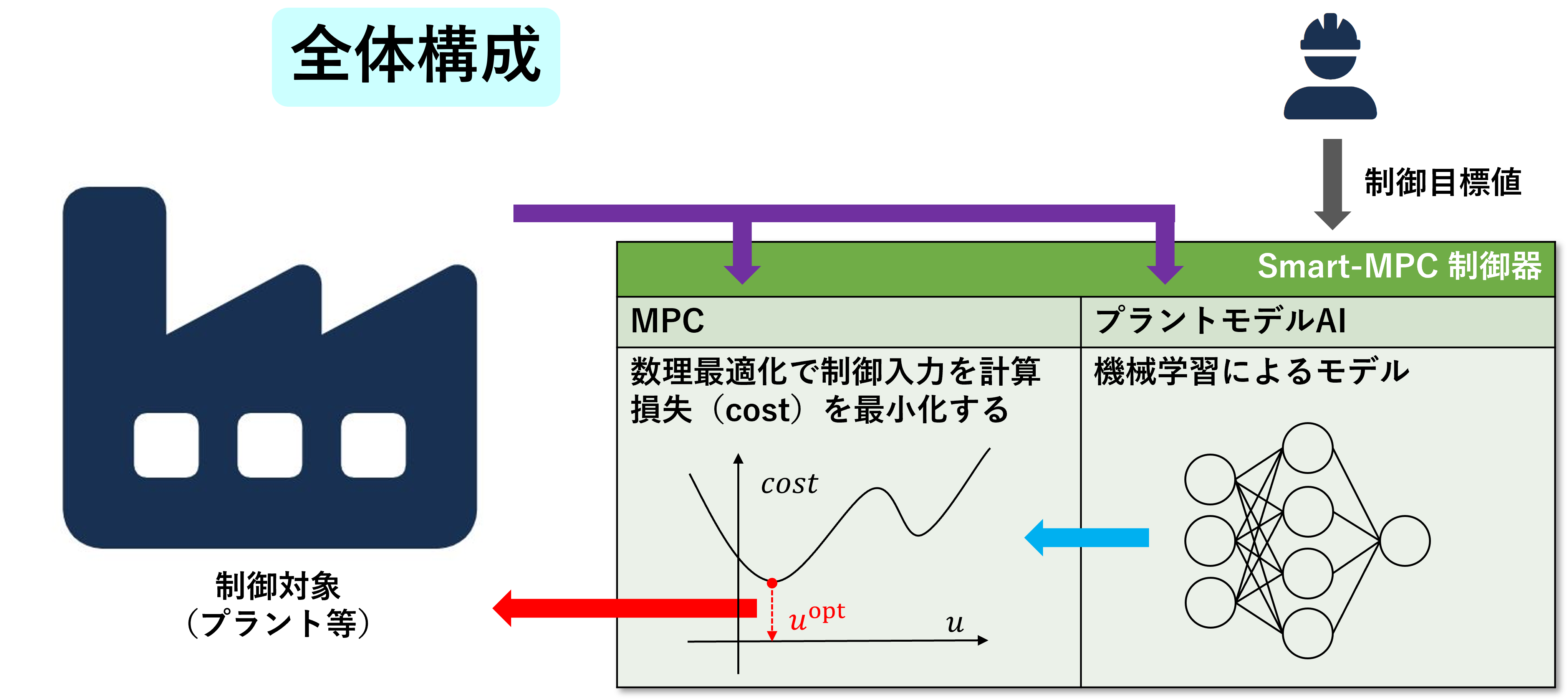
制御システムは制御対象(プラント等)と制御器の2つの要素から構成されています。 制御器の中にはプラントのダイナミクスを模倣するための機械学習モデルと、 MPC(モデル予測制御)に用いるための数理最適化ソルバーが存在します。
機械学習で得られたモデルはMPCの計算に使われ、毎ステップ(例えば10秒ごと)に 最適な制御入力\(u^{\rm{opt}}\)を計算し、プラントに渡します。
オンライン学習
制御入力は一定の周期でプラントに送られ、それに対するプラントの応答の情報が得られます。 入力+応答のペアが学習用データであり、 各ステップごとに得られる新しいデータを学習器にオンライン学習させることでリアルタイムに性能を改善していきます。
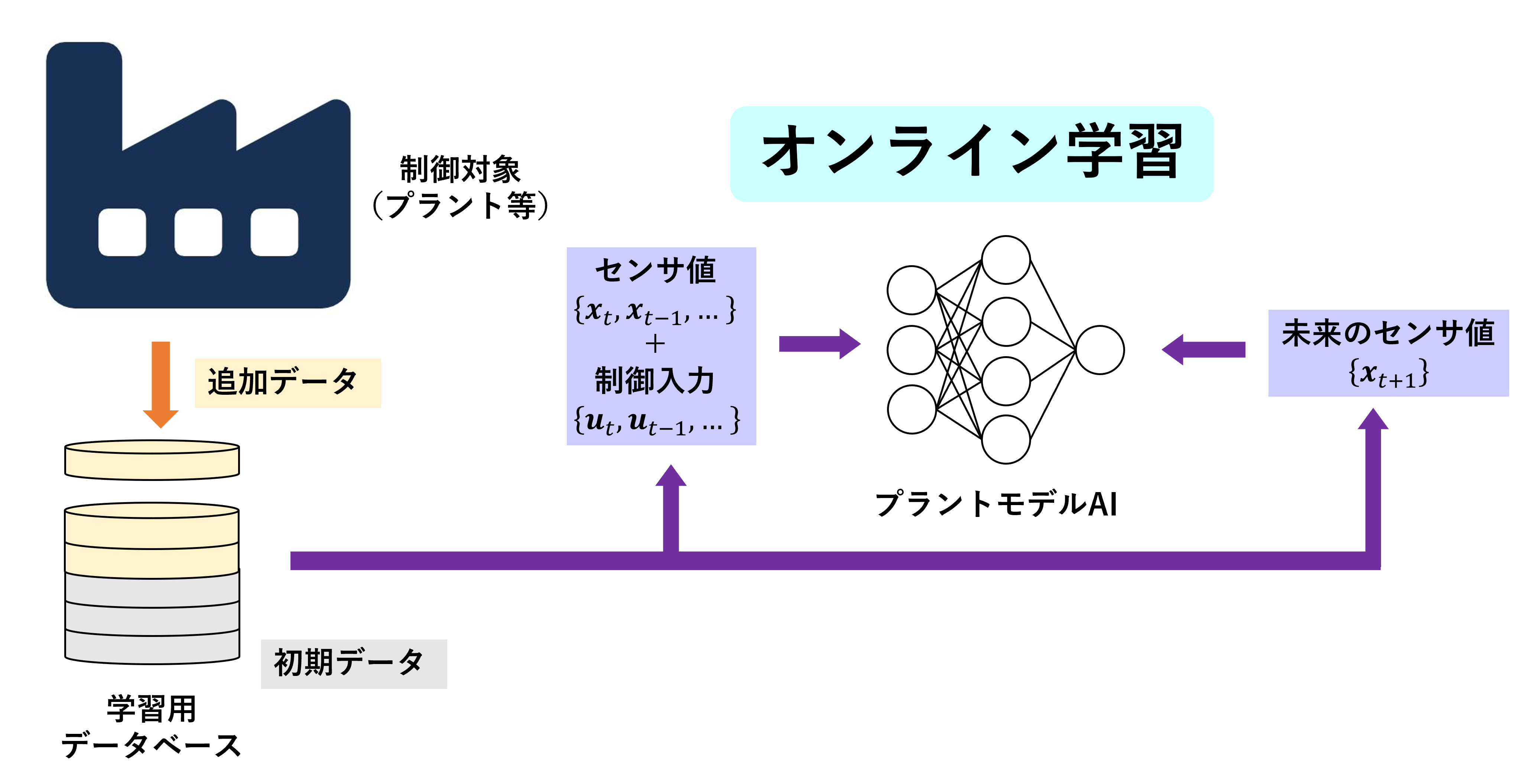
オンライン学習を用いることで性能の改善のみでなく、季節変動や経年劣化などの環境の変化にも適応出来るようになっています。
モデル予測制御
モデル予測制御は、制御したい対象の未来の状態(予測)に基づいて制御を行う手法です。
その長所としては以下のようなものがあげられます。
- 多入力多出力(MIMO)系を扱える
- 拘束条件が扱える
- 未来予測に基づいているため、むだ時間や応答の遅れに強く、オーバーシュートやハンチングを起こしにくい
- 最適な制御が可能
- 比較的ロバストで、モデル誤差などにも強い
この制御のアルゴリズムは2つの要素からなります。
1つ目は予測を行うためのモデルで、時刻\(t\)の状態変数\(\bm{x}_t\)、制御変数\(\bm{u}_t\)に対して
\[ \bm{x}_{t+1} = \bm{f}(\bm{x}_t, \bm{u}_t) \]
によって次の時刻\(t+1\)の状態を予測します。 これはプラントの運動方程式とも言え、通常のMPCでは物理モデルからこの方程式を導出します。この導出過程を機械学習によって自動化したのがSmart MPCです。
2つ目は評価関数Jであり、ステージコスト\(L\)(Lagrange term)と終端コスト\(\phi\)(Mayer term)を用いて
\[ J = \phi(\bm{x}_T) + \sum_{k=0}^{T-1} L(\bm{x}_{t+k}, \bm{u}_{t+k}) \]
と与えられます。
各時刻\(t\)毎に、この評価関数\(J\)を拘束条件下で最小にする制御軌道\(\{\bm{u}_t, \bm{u}_{t+1},\dots \}\)を計算し、\(\bm{u}_t\)を入力にします。
各時刻での入力\(\bm{u}_t\)を求めるために毎回時間幅\(T\)分の軌道の最適化問題を解かなければならないため、計算量は非常に多くなります。
しかしながら、近年では計算機の進歩によってRaspberry Piに搭載されているのCPU程度の能力でもリアルタイムにこの最適化問題を解きながら制御することが可能になってきました。
この最適化問題は制御変数\(\bm{u}\)に対する不等式制約を\(g_i, (i=1,2,\dots)\)とすると
\[ \min_{\{ \bm{x}_k, \bm{u}_k \}} J \] \[ s.t. \left \{ \begin{aligned} \bm{x}_{t+1} & = \bm{f}(\bm{x}_t, \bm{u}_t) \\ g_i(\bm{u}_k) & < 0, \ \ \forall k, \ \ i=1,2,\dots \end{aligned} \right . \]
と表せます。(簡単のため \(t=0\)とする)
拡張ラグランジュ法を用いて解くならラグランジュ乗数を\(\bm{\lambda}_k\),\(\rho_{ik}\)とすると
\[ \begin{aligned} J_\alpha & = J \\ & + \sum_{k=0}^{T-1} \left [ \bm{\lambda}^T_k \left( \bm{f}(\bm{x}_k, \bm{u}_k) - \bm{x}_{k+1} \right) + \frac{\alpha}{2} \left \| \bm{f}(\bm{x}_k, \bm{u}_k) - \bm{x}_{k+1} \right \|^2 \right ] \\ & + \frac{\alpha}{2} \sum_i \sum_{k=0}^{T-1} \left [ \mathrm{relu} \left ( g_i(\bm{u}_k )+ \frac{\rho_{ik}}{\alpha} \right )^2 - \frac{\rho^2_{ik}}{2 \alpha} \right ] \end{aligned} \]
\[ \begin{aligned} J_\alpha & = J \\ & + \sum_{k=0}^{T-1} \left [ \bm{\lambda}^T_k \left( \bm{f}(\bm{x}_k, \bm{u}_k) - \bm{x}_{k+1} \right) \right . \\ & + \left . \frac{\alpha}{2} \left \| \bm{f}(\bm{x}_k, \bm{u}_k) - \bm{x}_{k+1} \right \|^2 \right ] \\ & + \frac{\alpha}{2} \sum_i \sum_{k=0}^{T-1} \left [ \mathrm{relu} \left ( g_i(\bm{u}_k )+ \frac{\rho_{ik}}{\alpha} \right )^2 - \frac{\rho^2_{ik}}{2 \alpha} \right ] \end{aligned} \]
\[ \begin{aligned} \bm{x}_k, \bm{u}_k & \leftarrow \argmin_{\bm{x}_k, \bm{u}_k} J_\alpha \\ \bm{\lambda}_k & \leftarrow \bm{\lambda}_k + \alpha \left( f(\bm{x}_k, \bm{u}_k) - \bm{x}_{k+1}\right) \\ \rho_{ik} & \leftarrow \rho_{ik} + \alpha g_i(\bm{u}_k) \end{aligned} \]
を繰り返すことで解が得られます。
\(g_i\)が連続微分可能ならば\(\mathrm{relu} \left( g_i(\bm{u}_k) + \frac{\rho_{ik}}{\alpha} \right)^2 \)も連続微分可能なので勾配法やニュートン法等を用いて(局所)最小化できます。
強化学習との比較
Smart MPCはデータからモデルを構築・学習しながら、上記のMPCのアルゴリズムによって制御を行います。 一方でAlphaGoやDQNのような(モデルフリーの)強化学習には、モデルという概念が存在せず、ダイナミクスの学習と行動の決定はすべてQ関数に押し込められています。
本来、状態の価値がわかることと、未来が予測できるかどうかということは別問題であり、これらは分割して解くことが可能であると考えられます。 強化学習を難しくしている原因の一つが、この2つの異なる問題を一気に解こうとしているためであり、Smart MPCではこれらを個別に解くことで学習を著しく簡単かつ安定にすることが出来ました。
一方で、Smart MPCは評価関数は別個与えてやる必要があるため、評価関数が比較的自明に与えられる問題、例えば温度の乖離やエネルギーの消費量など、であれば適用可能ですが、それが不可能な問題、例えば囲碁や将棋など状態の評価自体が最も重要である問題に対しては直接的には使うことが出来ません。 Bonanzaメソッドのように過去のデータから逆最適化問題を解くことで評価関数を構成することは可能ですが、このタイプの問題には強化学習を使うことが最適であると思われます。
PID制御との比較
PID制御は現代において最も使われている制御手法であり、多くのプラントや機械の制御に使われています。 非常に単純なアルゴリズムであり挙動が理解しやすいため現場で作業者が調整を行いやすいというメリットがある一方で、以下ような欠点を持ちます。
- 一入力一出力(SISO)系しか扱えない。
- 拘束条件を扱えない。
- 学習機能はなく、すべて人間が調整する。
- パラメータの調整は系統的に行うことは難しく、一般的に勘と経験に基づいて行われている。
- 根本的にむだ時間に弱く、ハンチングやオーバーシュートを防ぐためにはスミス補償器のような補助的な機器を用いる必要がある。これはPIDの長所である理解のしやすさを損なわせるものである。
Smart MPCは上記すべての欠点を克服することが可能であり、一方でPID制御に決して劣らない手軽さやわかりやすさを備えています。