教師がいらないもう一つのニューラルネットワーク
Sparse Competitive Network
SCN
SCN(Sparse Competitive Network)とは弊社が開発した独自のアルゴリズムで、オンラインの教師なし学習を行うニューラルネットワークです。 SCNはいわゆるディープラーニングのように誤差逆伝播法によって学習するのではなく、競合学習(Competitive Learning)と呼ばれる方法で学習します。
競合学習による学習は逆伝播と比べると計算量・メモリ消費量、共に非常に小さいので、SCNはスマートフォンやマイコンのような計算資源が限られた環境でも十分動作します。
このアルゴリズムは元々スパースコーディング(Sparse Coding)と呼ばれる教師なし学習のアルゴリズムを高速に近似する方法として開発されました。
スパースコーディングの少数データでも高い性能が出せるという特徴のおかげで、SCNを用いたCentauri Liteは数枚の画像から運用が可能になりました。
競合学習
競合学習はHebb則(Hebbian Learning)と呼ばれるルールに基づく機械学習アルゴリズムです。 Hebb則は1949年に神経細胞の学習則として心理学者Donald Hebbらによって提唱されたもので、そのもとではニューロンは入力された信号をより強化するように学習します。 つまり同じ信号が二回入力されれば、二回目の出力は一回目のそれより強くなります。
Hebb則は1個1個のニューロンの学習則ですが、競合学習はこれをニューラルネットワークに拡張したものです。
競合学習ではニューロンの出力に着目し、それらを比較します。そしてその中で最も出力が強いものを勝者(winner neuron)と呼び、そのニューロンに対してHebb則を適用します。これを勝者総取り則(winner-take-all rule) と呼びます。
この競合学習に基づくアルゴリズムとしては以下のような手法がよく知られています。
自己組織化写像(SOM)
データを可視化するニューラルネットワーク
自己組織化写像(SOM: Self Organizing Map)は大脳皮質の視覚野の振る舞いを参考にT. Kohonenによって1982年に開発されたアルゴリズムです。高次元のデータを低次元(1~3次元)に落とし可視化することができます。
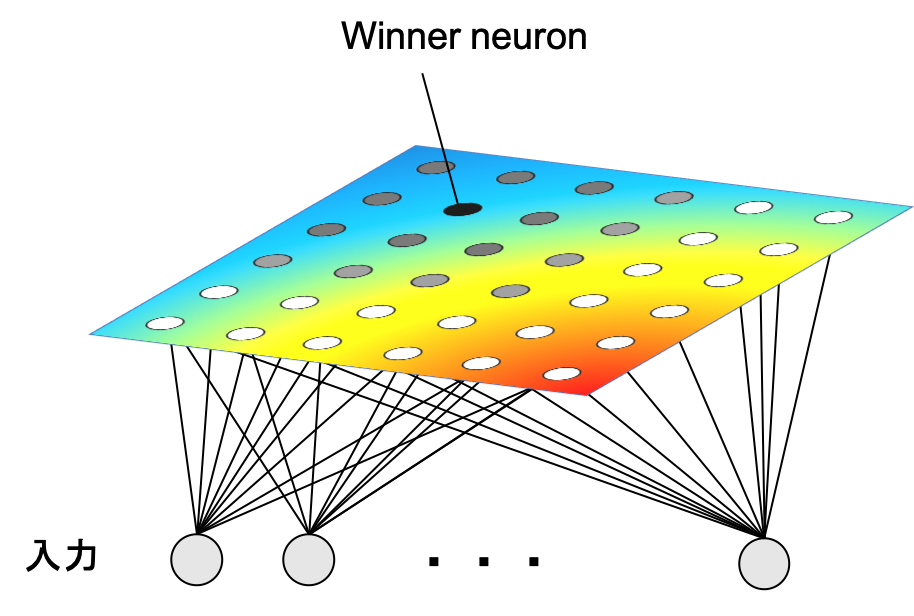
自己組織化写像は高次元データの低次元の構造を位相を保ったまま可視化することができるので、主成分分析やt-SNEのような多様体学習の手法とともにデータの分析や次元削減などに用いられます。
ネオコグニトロン
競合学習によるディープラーニング
ネオコグニトロン(Neocognitron) は福島邦彦氏によって1979年に発表された多層のニューラルネットワークで、現在の畳み込みニューラルネットワークの原型にあたるアルゴリズムです。
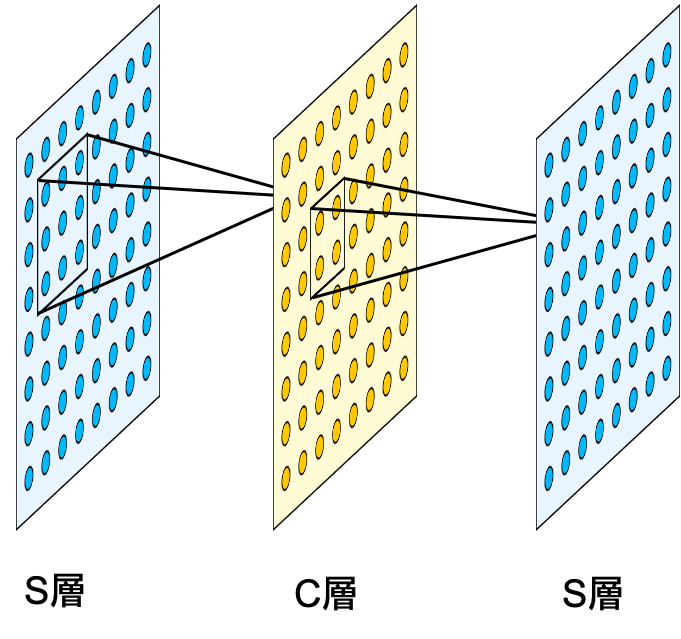
ネオコグニトロンは手書き文字の分類問題において精度98.6%という高い識別性能を出し、“階層的に局所的な特徴量の抽出を重ねる”、 “プーリングによって平行移動に対するロバスト性を高める”といった後にディープラーニングにおいて重要な役割を果たす概念の正しさを実証しました。
スパースコーディング
スパースコーディングはスパースモデリングと呼ばれるアルゴリズムの一つで、上述した競合学習と同様に大脳皮質の視覚野の振る舞いをもとに考え出されました。 このアルゴリズムは入力された信号をなるべく少ないパーツの組み合わせで表現することを目的とします。
大脳皮質の学習過程では、学習を始めたばかりのころは多くの神経細胞が発火していますが、習熟度が上がるにつれてだんだん発火の量が減っていくことが知られています。(*)
これは直感的には、「より少ない“言葉数” で物事を表現できるとき、より本質的な理解ができている」あるいは「的確に現象を表現できる“よい言葉”を獲得できた」等のように言い換えられるかもしれません。
このような考え方は機械学習の分野だけでなく昔から様々な領域において支持されてきました。 例えば物理学の世界ではなるべく単純なルール(方程式)を採用した理論が結果的に正しい、 といったことがしばしばあり指導原理の一つとしてオッカムの剃刀と呼ばれる考え方が時折引用されます。
アルゴリズムとしてのスパースコーディングは「入力信号をなるべく少ない基底の線形和で再構成する」という最適化問題(教師なし学習)として定式化されます。これは辞書学習とも呼ばれ、具体的には以下の形で与えられます。
入力データ: \( \bm{x}_{i} \) , 出力: \( Y=\left\{ \bm{y}_{1},\ldots ,\bm{y}_{N}\right\} \)
基底: \( D=\left[ \bm{d}_{1},\ldots ,\bm{d}_{n}\right] \)
\[ \min _{D, Y}\sum _{i} \dfrac {1}{2}\left\| \bm{x}_{i} - D \bm{y}_{i} \right\| ^{2}_{2} +\lambda \left\| \bm{y}_{i}\right\| _{1} \]
\[ s.t. \ \ \ \ \ \sum _{j}D^{2}_{kj}\leq c \ (\forall k=1,2,\ldots,n), \ \ c > 0, \ \ \lambda > 0 \]
\[ s.t. \ \ \ \ \ \sum _{j}D^{2}_{kj}\leq c \ (\forall k=1,2,\ldots,n), \] \[ \ \ c > 0, \ \ \lambda > 0 \]
様々な自然画像から切り出した9×9の画像パッチの集団に対してスパースコーディングを適用した例を下に示しました。

右の64枚の画像はそれぞれ学習された基底(画像)で、それらのうちわずか4枚の組み合わせで左の人物の口角の辺りの画像パッチを再構成しています。
このようにして得られた出力yは「良い」性質を持っていることが知られています。例えば、画像に対してスパースコーディングを畳み込みのように実行し、得られたyのmapを画像の特徴量として分類問題を解くと高い性能が出せるということが知られています。
* https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0068705スパースコーディングの問題点
上述のようにスパースコーディングを用いれば教師なしでデータからよい特徴量が取り出せますが、一方でこのアルゴリズムには大きな問題点があります。それは学習だけでなく推論にも非常に時間がかかるというものです。
その原因は、スパースコーディングはニューラルネットワークやPCAなどとは違い、逆問題として定式化されているという所にあります。
ニューラルネットワークの推論
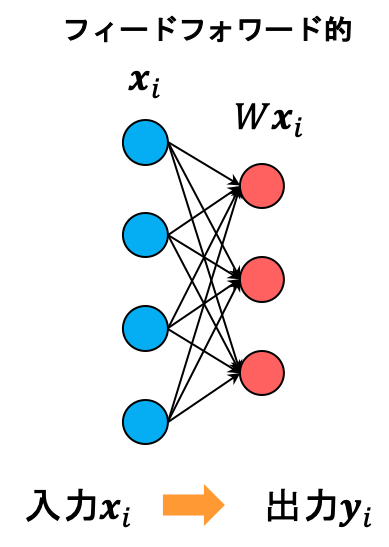
スパースコーディングの推論
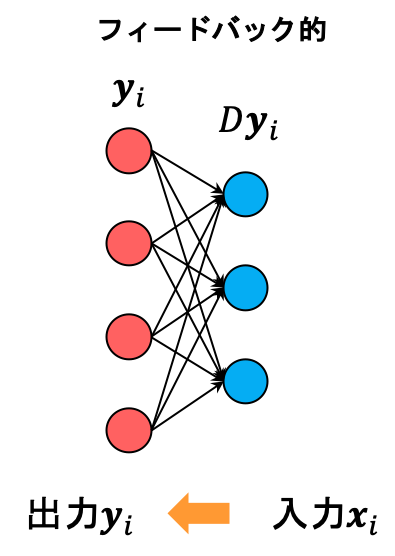
ニューラルネットワークの推論は入力に対し一度行列をかけて非線形な活性化関数をかけるだけで済みます。
一方でスパースコーディングの推論はたとえ学習が完了している、すなわちDが与えられているような場合であっても上の式を陽に解くことはできません。 これはつまり、推論するたびに勾配法のような反復的な手法を用いて計算をしなければならないことを意味しています。
このような問題点を解決するために弊社が考案した手法がSCN(Sparse Competitive Network)です。
SCNのアルゴリズム
高速なスパースコーディング
SCNはスパースコーディングの近似法の研究から生み出されました。 この方法では反復法に頼ることなく、1層のニューラルネットワークのように行列演算と非線形な活性化関数の組み合わせのただ一回の計算で推論が可能です。
高速に推論を行うことができるため、それによって学習の高速化も可能になりました。
この近似アルゴリズムが実は競合学習とも深い関係にあることから、我々はこれにSCN、すなわちスパース競合ネットワークという名前を付けました。
前述したようにスパースコーディング(辞書学習)では下記の最適化問題を解くことで、辞書Dとその時の推論yを得ます。
\[ \min _{D,Y}\sum _{i} L(D,\bm{y}_{i}) := \min _{D,Y}\sum _{i} \dfrac {1}{2}\left\| \bm{x}_{i}-D\bm{y}_{i}\right\| ^{2}_{2} + \lambda \left\| \bm{y}_{i}\right\| _{1} \]
\[ \min _{D,Y}\sum _{i} L(D,\bm{y}_{i}) \] \[ := \min _{D,Y}\sum _{i} \dfrac {1}{2}\left\| \bm{x}_{i}-D\bm{y}_{i}\right\| ^{2}_{2} + \lambda \left\| \bm{y}_{i}\right\| _{1} \]
しかしDとYを同時に得ることは難しいため、通常は片方を固定してもう片方の変数のみに関して最適化をするという計算を交互に収束するまで繰り返します。
ここでまず初めにYの計算(推論)のアルゴリズムについて、Proximal Gradient Method(近接勾配法)と呼ばれる手法についてみていきます。
Proximal Gradient Method(近接勾配法)
Dが与えられていて、yについて最適化問題を解くことを考えます。この時、目的関数は以下に示すように二つの部分から成り立ちます。
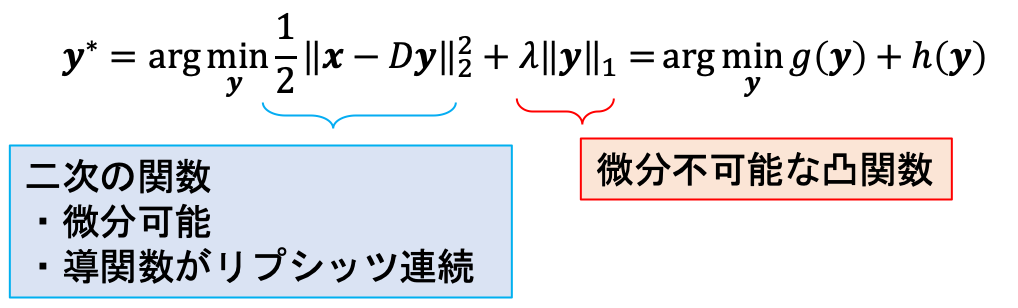
第一項\(g(\bm{y})\)(誤差の損失項)は二次の関数なので微分可能で、その導関数もリプシッツ連続です。第二項\(h(\bm{y})\)(正則化項)は微分不可能な凸関数です。
第二項\(h\)が微分不可能なので勾配法は使えませんが、このような条件を満たすとき、proximal gradient method(PGM: 近接勾配法)と呼ばれる方法を用いて最適化が可能になります。
まず初めに、次のようなprox作用素と呼ばれる作用素を導入します。
\[ \mathrm{prox}_{f}\left( \bm{x}\right) :=\argmin_{\bm{u}} \left\{ f\left( \bm{u} \right) +\dfrac {1}{2} \left\| \bm{u} - \bm{x} \right\| ^{2}_{2}\right\} \]
\[ \mathrm{prox}_{f}\left( \bm{x}\right) \] \[ :=\argmin_{\bm{u}} \left\{ f\left( \bm{u} \right) +\dfrac {1}{2} \left\| \bm{u} - \bm{x} \right\| ^{2}_{2}\right\} \]
( ただし \(f\)は任意の凸関数 )
prox作用素は凸関数\(f\)の形によっては解析的に解くことができます。特にL1ノルムの時( \(f(\bm{u}) = \left\| \bm{u} \right\|_{1} = \sum_i \left| u_i \right| \) )は以下に示すように、 各成分\(j\)ごとに問題を分解し、その劣微分を0とおくと解けます。 絶対値関数\(|t|\)の劣微分は
なので、
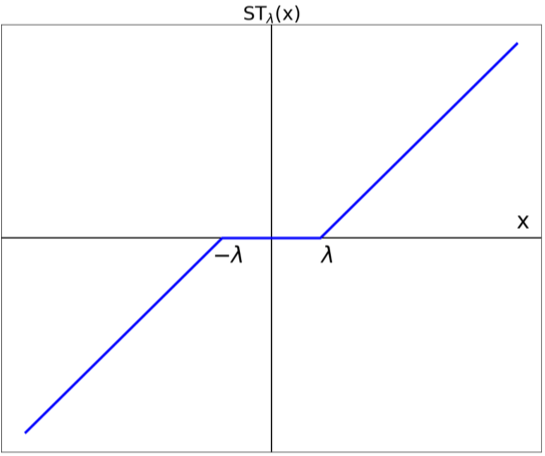
を解くと以下のようにソフト閾値関数STを用いて表せます。
\[ \left[ \mathrm{prox}_{h}\left( \bm{x} \right) \right] _{j} = \mathrm{ST}_{\lambda }\left( x_{j}\right) :=\begin{cases} x_{j}+\lambda , & x_{j} <-\lambda \\ 0, & -\lambda \leq x_{j}\leq \lambda \\ x_{j}-\lambda, & \lambda < x_{j} \end{cases} \]
\[ \left[ \mathrm{prox}_{h}\left( \bm{x} \right) \right] _{j} = \mathrm{ST}_{\lambda }\left( x_{j}\right) \] \[ :=\begin{cases} x_{j}+\lambda , & x_{j} <-\lambda \\ 0, & -\lambda \leq x_{j}\leq \lambda \\ x_{j}-\lambda, & \lambda < x_{j} \end{cases} \]
このprox作用素を用いて、PGMによる推論ステップは以下のようにあらわせます。
( \(\alpha\) は小さい正の実数、学習率に対応 )
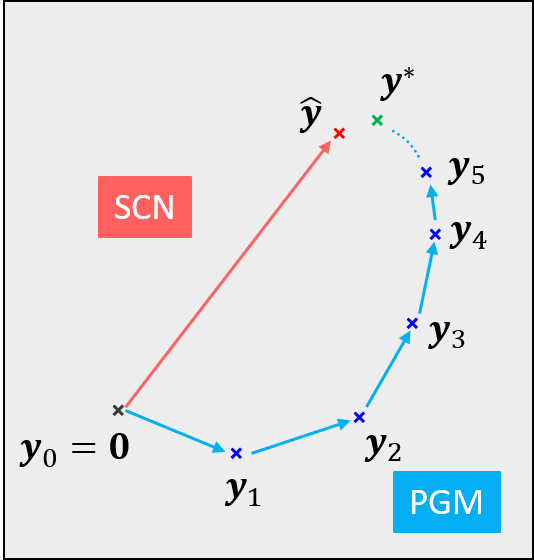
PGMは上記のステップを収束するまで繰り返すことにより、推論\(\bm{y}^∗\)を得ます。
SCNの推論アルゴリズム
SCNの推論アルゴリズムはPGMの反復計算をいくつかの仮説と数学的なテクニックによって近似することで導かれました。
近似解\(\widehat{\bm{y}}\)は次のように表せられます。
ただし、\(\phi\)はパラメトリックな非線形関数、\(W\)は行列であり、共に\(D\)と\(\lambda\)から解析的に求めることができます。
この近似のおかげで推論過程がフィードフォワードのニューラルネットワークと等価なモデルに置き換えることができ、 SCNの非常に高速な推論が実現できました。
競合学習によるSCNの学習
学習はSGD(確率的勾配法)によって実行され、その更新則は以下のようになります。
\(\otimes\)はテンソル積(外積)、 \(\eta \left( > 0 \right) \)は学習率
この時、推論\(\bm{y}\)はスパースな解であるので\(\bm{y}\)の成分の内ごく少数のみが値を持ち、それ以外の成分は0をとります。
したがって、\(\bm{y}\)を絶対値が大きな上位\(k\)個の成分だけで近似することが可能になります。ここでは簡単のために、最も強い近似である\(k=1\)のパターン(winner-take-all)のみを考えます。
最上位の成分を\(s\)とすると
とでき、更新則は次のように書き換えられます。
これはまさに競合学習による更新則であり、SCNの学習則はこのようにして導かれます。
実際には上記の更新則にDに対する正則化項やmomentum項などを追加することで、SCNはより安定かつ高速な学習を実現しています。
SCNでできること
豊富なソリューション
SCNはそのスパース性とモデルのシンプルさから非常に多くのソリューションを提供することができます。
その中でも代表的な応用先を以下に4つほどご紹介いたします。
I. 教師なし異常検知
一般的に機械学習における最適化問題は、それに対応する確率モデルの最尤推定の問題に変換することができます。
SCN(およびスパースコーディング)は前述した損失関数を対数尤度であるとみなすと次のような確率モデルに対応付けられます。
このように計算される負の対数尤度Lを、入力信号\(\bm{x}\)の「新規性」として用いることで異常検知を行うことができます。
・正常データのみを教える場合
Centauri Liteは正常画像のみを教えることで異常検知を行います。 ここでは例として、整列させたアーモンドに混入した異物を検出するようなパターンを見てみます。

学習には正常画像のみを用い、またその際に正常データ内における新規性の最大値も
として計算しておきます。これを基準にして、検出の閾値を実数\(\alpha\)を用いて
として与えます。なお、少々紛らわしいですが、Centauri Lite内ではこの\(\alpha\)を検出閾値(許容度)と呼んでいます。
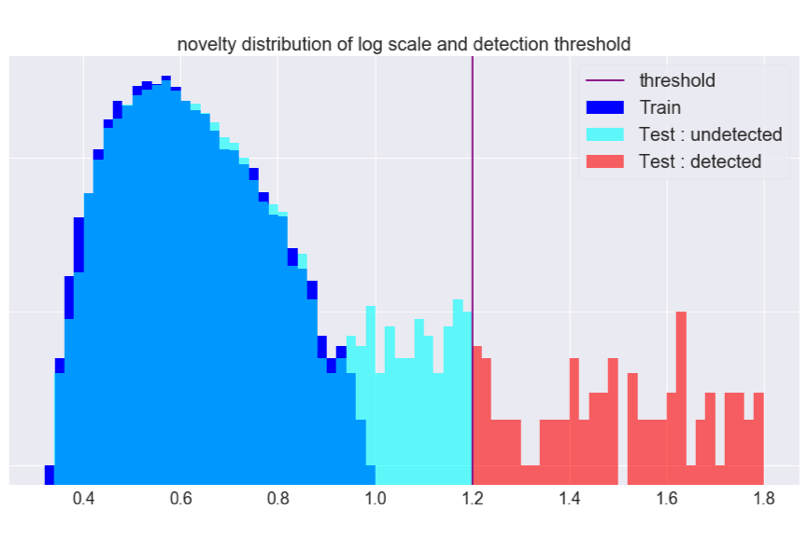
上の図は新規性のヒストグラム(対数スケール)で、青は正常画像(学習データ)、 水色と赤は異常が含まれる画像(テストデータ)に対応します。 後者はわかりやすさのために閾値の前後で色が分けてあります。
横軸は新規性を表していて、\(\mathrm{NovMax}=1\)になるように規格化されています。
今回の例は\(\alpha=0.2\)の場合に対応しますが、\(\alpha\)を小さくしていくことで検出の感度を上げたり、 またその逆を行ったりすることで適切な閾値を設定できます。
・異常も含め、全データを教える場合
Centauri Lite のようにスマートフォン上でユーザーがインテラクティブに正常データを教えられる場合は先ほどのやり方でも十分ですが、一方でCentauri Nanoのようにマイコンなどのエッジ上での異常検知を行う場合、常に張り付いて教えるというわけにもいきません。
この場合も先ほどと同様の方法で異常検知が可能ですが、異なる点として\(\mathrm{NovMax}\)の代わりに以下の式で計算される\(\theta_\mathrm{max}\)を導入します。
\[ \int _{L\left( \bm{x} \right) \leq \theta _\mathrm{\max }} p \left( \bm{x} \right) d\bm{x} = \int ^{\theta _\mathrm{\max }}_{0}p_\mathrm{nov}\left( \nu\right) d\nu=0.99 \]
\[ \int _{L\left( \bm{x} \right) \leq \theta _\mathrm{\max }} p \left( \bm{x} \right) d\bm{x} \] \[ = \int ^{\theta _\mathrm{\max }}_{0}p_\mathrm{nov}\left( \nu\right) d\nu=0.99 \]
\(\mathrm{NovMax}\)は今までに観測した最大の新規性のことでしたが、\(\theta_\mathrm{max}\)は 「今までに観測した新規性の\(99%\)が\(0 \sim \theta_\mathrm{max}\) に含まれる」という意味になります。
この変更によって、外れ値に対して閾値が頑強になり異常データごと学習が可能になります。なお、\(0.99\)という数字は運用に合わせて適切に選ぶこともできます。
II. ノイズ除去&信号分離
カクテルパーティーのように同時にたくさんの人が会話していて、さらに雑音も多いという環境でも、人間の耳は特定の人の発言にフォーカスし内容を聞き取ることができます。 あるいは、訓練された人であれば音楽から特定の楽器の音だけを抽出し、その楽譜を作成したりすることもできます。
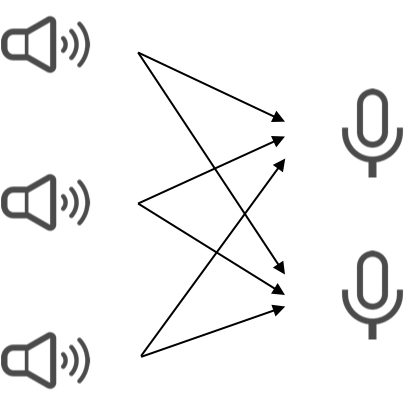
このように混合した信号を分離する問題を解く方法として独立成分分析と呼ばれる手法が知られています。
SCN、およびスパースコーディングを用いることで高い精度でこの問題を解くことができます。
III. 圧縮センシング
欠損した情報から元の情報を高い精度で再構成する技術である、圧縮センシングと呼ばれるアルゴリズムが近年注目を集めています。
圧縮センシングという名前の由来は、センシング(測定)を減らすという所から来ていて、これは言い換えれば測定を上手く“間引く”というような概念に近いかもしれません。
一回の測定に時間やコストなどがかかったり、あるいはそもそもあまり測定回数を増やせないような状況において、効果的に間引いた測定を行い、後で高い精度での再構成を目指します。
圧縮センシングのイメージ

圧縮センシングによって欠損した情報が復元できる理由は、観測されうる信号に何らかの仮定がおける場合が多いからです。 例えば画像データの場合「あるピクセルとその隣のピクセルの値は似ている」、といった空間方向に対する相関の強さなどが知られています。
これはベイズ理論の枠組みでは観測データの事前分布の推定の問題に帰着されます。 この事前分布に関して様々が研究されていて、スパースランドモデルや、 最近強い注目を集めた Deep Image Priori など、様々な理論が提唱されています。
圧縮センシングが産業向けのソリューションとして最も成功したのはおそらく医療用MRIへの応用例でしょう。
MRI装置
人の頭部MRIの模式図
( Shepp–Logan phantom )
観測信号\(\bm{x}\)の次元\(d_{x}\)に対し、再構成する画像\(\bm{y}\)の次元\(d_{y}\)は
を満たすとします。この時、\(\bm{x}\)の情報量が少ないので\(\bm{y}\)を\(\bm{x}\)から求めることは一般的にはできませんが、 この信号\(\bm{x}\)がMRIの観測データで、欲しい画像\(\bm{y}\)がMRIの画像であることはわかっているので、 \(\bm{y}\)の事前分布を与えることができます。 これは正則化項を含めた形として以下の式を最適化問題に帰着できます。
\[ \min _\bm{y}L\left( \bm{y}\right) = \min _\bm{y}\dfrac {1}{2}\left\| \Phi \left( \bm{y}\right) -\bm{x}\right\|^{2}_{2} + \lambda \left\| \psi \left( \bm{y} \right) \right\| _{1}+\mu \left\| \bm{y} \right\| _{TV} \]
\[ \min _\bm{y}L\left( \bm{y}\right) = \] \[ \min _\bm{y}\dfrac {1}{2}\left\| \Phi \left( \bm{y}\right) -\bm{x}\right\|^{2}_{2} + \lambda \left\| \psi \left( \bm{y} \right) \right\| _{1}+\mu \left\| \bm{y} \right\| _{TV} \]
ただし、\(\Phi\)はフーリエ変換、\(\psi\)はウェーブレット変換、\(\left\| \cdot \right\| _{TV}\)は全変動ノルム
この技術によってMRIの検査は非常に高速化され、患者への負担を減らし、特に救命救急のように一刻を争う状況においてその真価を発揮しました。
また、宇宙物理学の分野においても圧縮センシングは大きな注目を集めており、最近ではブラックホールの画像をスパースな観測データから再構成することに成功しました。
ブラックホールの可視化に使われたCHIRP (Continuous High-resolution Image Reconstruction using Patch priors)と呼ばれるアルゴリズムは事前分布として混合ガウス分布を仮定し、最適化問題を解きます。
この技術によって高解像度なブラックホールの写真を撮影することが可能になりました。
IV. ロバスト最適制御
機械の「良い操作」とはどのようなものを指すのでしょうか?
一般的に言えば、熟練した人ほど無駄な動きが少なく、必要最小限の操作だけをする傾向があります。
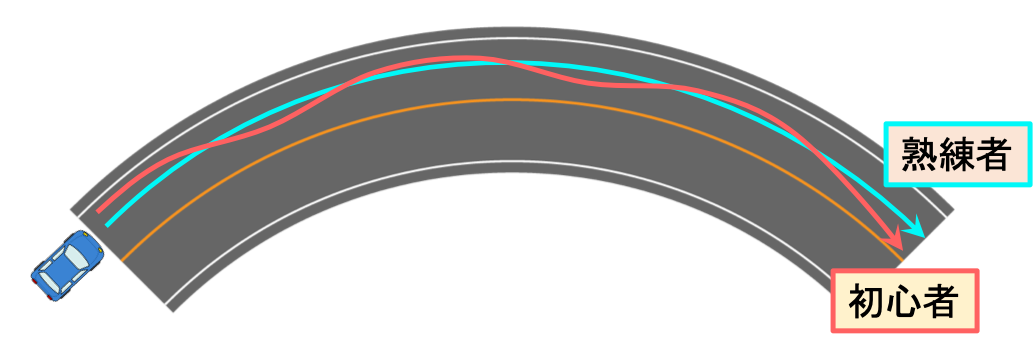
車の運転を例にとると、カーブを曲がるとき初心者は何度もハンドルやブレーキを操作するため軌道が不安定なものになってしまいがちですが、熟練者は少ない操作で安定した軌道を描くことができます。
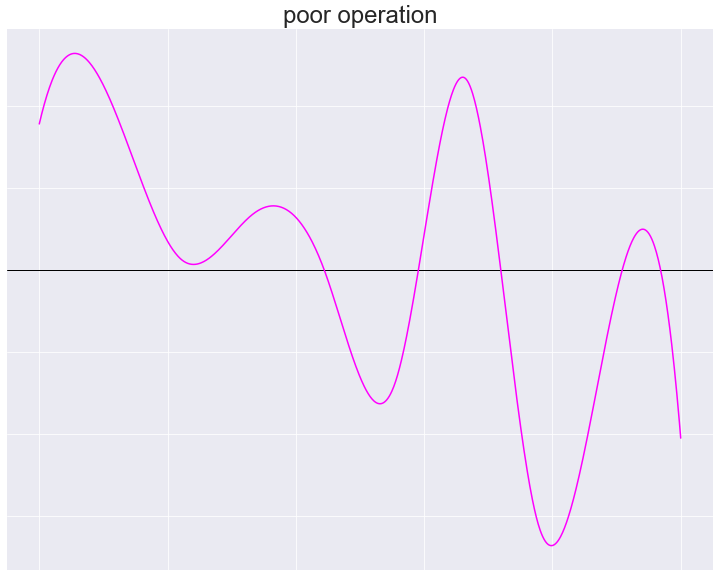
初心者による“悪い”操作パターンの例
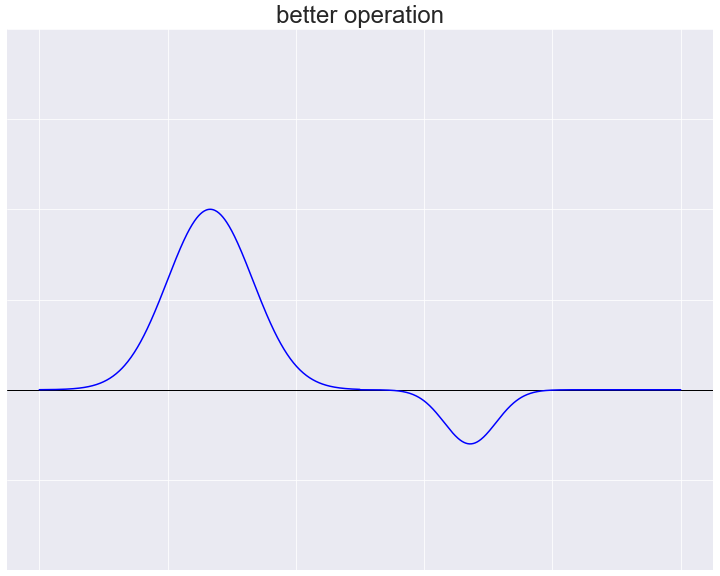
熟練者による“良い”操作パターンの例
つまり“良い”制御とは、アクセルやハンドルのような制御変数\(u\left(t\right)\)やその微分\(\Delta u\left(t\right)\)がスパースであると言い換えられます。
この考え方は制御工学の観点からも支持されていて、制御入力がスパースになるようなアルゴリズムを用いると、 高いエネルギー効率と外乱や観測誤差などに対するロバスト性が得られることが知られています。
SCNの計算の軽さによって、このような制御がエッジにおいて可能になります。
