かすかなヒントから真実を見つける
圧縮センシング
圧縮センシングとは?
圧縮センシングは少ない観測データから元の信号を復元する方法で、名前の由来は観測(センシング)を間引く(圧縮する)ことから来ています。 MRIを中心に医療技術や宇宙探査など様々な分野で用いられており、この技術はとりわけ1回あたりの観測コストが高いようなタスク、 あるいは観測回数を減らすベネフィットが大きいタスクなどに対してその真価を発揮します。
欠損した信号の復元が可能な理由は、観測される信号には事前にある程度パターンが予測できる場合があるからです。 すなわち、画像には「画像らしさ」が、音声には「音声らしさ」があり、欠損した情報を補うことができるということが知られています。 これは人間を含めた生物の脳が自然に行っていることであり、それを数理的なアルゴリズムに置き換えたものが圧縮センシングです。
スパース性の仮定
それでは、「らしさ」・「らしくなさ」とは何でしょうか?画像を例にして考えてみましょう。

宇宙飛行士

白色ノイズ
1番目の画像は非常に画像らしさを持ったデータですが、 2番目のそれは画像として普段目にするパターンから大きく外れたあまり「らしくない」データであるといえます。
この2つのデータの違いに見えるように、情報の「それらしさ」というのはよく知っているパターンの組み合わせで表すことが可能である、 すなわち「少数の要素へ分解できること」だ、という考え方があります。
少数の組み合わせ、すなわちスパースな表現が可能であるということがスパース性の仮説であり、 そのような信号の生成モデルをスパースランドモデルと呼びます。
この「スパース性の存在」という仮定は観測データに欠損がある際に非常に強力なヒントになります。
画像の持つ性質と
スパース性
画像が普遍的に持っている性質として以下のようなものが知られています。
- ある画素の隣の画素は似ていることが多い。つまり画素値の低周波成分が強く、画素間の局所相関が高い。
- 画素値が急に変わる部分、つまりエッジのような部分は1次元的に連続してつながっていることが多い。
- 画素値の変化は写っている物体それぞれの場所とスケールに応じている。
これらの性質は画像の「全変動」と「ウェーブレット変換」に対するスパース性として現れることが知られています。
最適化問題としての
圧縮センシング
圧縮センシングを使えば欠損ありの画像に対して、再構成画像を生成することができます。 この際、再構成画像は「観測された画素値をなるべく再現しながら同時に先ほどのスパース性を満たす」ように選ばれます。
これはL1正則化を用いた最適化問題として定式化することができます。
再構成画像の画素値、およびそれを1次元ベクトルに並び替えたものを\(\phi\)とすると全変動\(\Psi_{TV}\)(差分フィルタ)は
\[ \Psi_{TV}(\phi)= \begin{pmatrix} \partial_{x}\phi \\ \partial_{y}\phi \end{pmatrix} \]
で与えられます。 正則化係数\(\alpha\)、ウェーブレット変換\(\Psi_{W}\)、観測画素の1次元ベクトル\(\eta\)、 \(\phi\)に対するサンプリング行列\(P\)を用いて損失関数\(L\)を
\[ L(\phi) = \|P\phi-\eta\|^{2}_{2} +\alpha_{W}\|\Psi_{W}(\phi)\|_{1} +\alpha_{TV}\|\Psi_{TV}(\phi)\|_{1} \]
\[ L(\phi) = \|P\phi-\eta\|^{2}_{2} \] \[ +\alpha_{W}\|\Psi_{W}(\phi)\|_{1} +\alpha_{TV}\|\Psi_{TV}(\phi)\|_{1} \]
とすれば上に述べた条件を見たす再構成画像はLの最小化問題を解くことで得られます。

64%の画素を間引いた画像

再構成された画像
ただ、この最適化問題は微分不可能なL1ノルムを含むため、勾配を用いた通常の最適化法を使うことができません。
ADMMによる最適化
このようなL1ノルムを含む損失関数を最適化する方法として、 FISTA、OWLQN、ADMM、DALなど様々なアルゴリズムが開発されています。 中でもADMM(Alternating Direction Method of Multipliers)は 調整パラメータの少なさや安定性の高さ、収束の速さ、適用可能問題の広さなど、 非常に使い勝手の良いアルゴリズムであり、我々は圧縮センシングのみならず 数多くのスパースモデリングの問題において標準的に採用しています。
ADMMによる更新の式は以下のように導かれます。 まず\(\Psi_{TV}\)、 \(\Psi_{W}\)は線形変換なので、行列Gを用いて
\[ \begin{pmatrix} \alpha_{W}\Psi_{W}(\phi) \\ \alpha_{TV}\Psi_{TV}(\phi) \end{pmatrix} =G\phi \]
と書くことができ、損失関数は
\[ L(\phi) = \| P\phi - \eta \|^2_2 + \| G\phi \|_1 \]
と書き換えることができます。 さらに新たな補助変数zとを用いれば最適化問題は
\[ \underset{\phi, z}{\rm{minimize}} \ L(\phi, z) = \underset{\phi, z}{\rm{minimize}} \ \| P\phi - \eta \|^2_2 + \| z \|_1 \] \[ s.t. \qquad G\phi = z \]
\[ \underset{\phi, z}{\rm{minimize}} \ L(\phi, z) \] \[ = \underset{\phi, z}{\rm{minimize}} \ \| P\phi - \eta \|^2_2 + \| z \|_1 \] \[ s.t. \qquad G\phi = z \]
として与えられます。
すると、拡張ラグランジュ関数は乗数\(\lambda\)と実数\(\rho \gt 0\)を用いて
\[ \mathcal{L}_\rho (\phi, z, \lambda) = L(\phi, z) + \lambda^T (G\phi - z) + \frac{\rho}{2} \| G\phi - z \|_2^2 \]
\[ \mathcal{L}_\rho (\phi, z, \lambda) = L(\phi, z) \] \[ + \lambda^T (G\phi - z) + \frac{\rho}{2} \| G\phi - z \|_2^2 \]
と書けます。
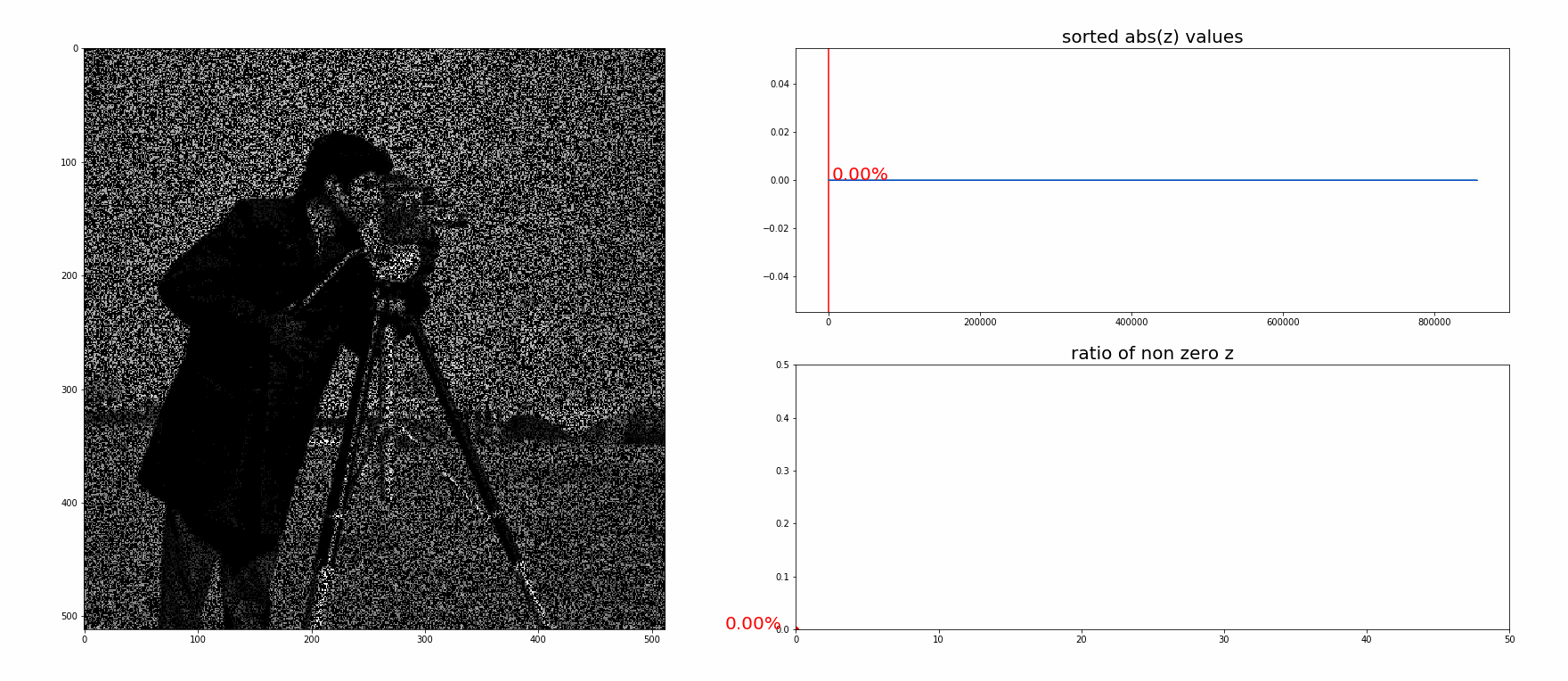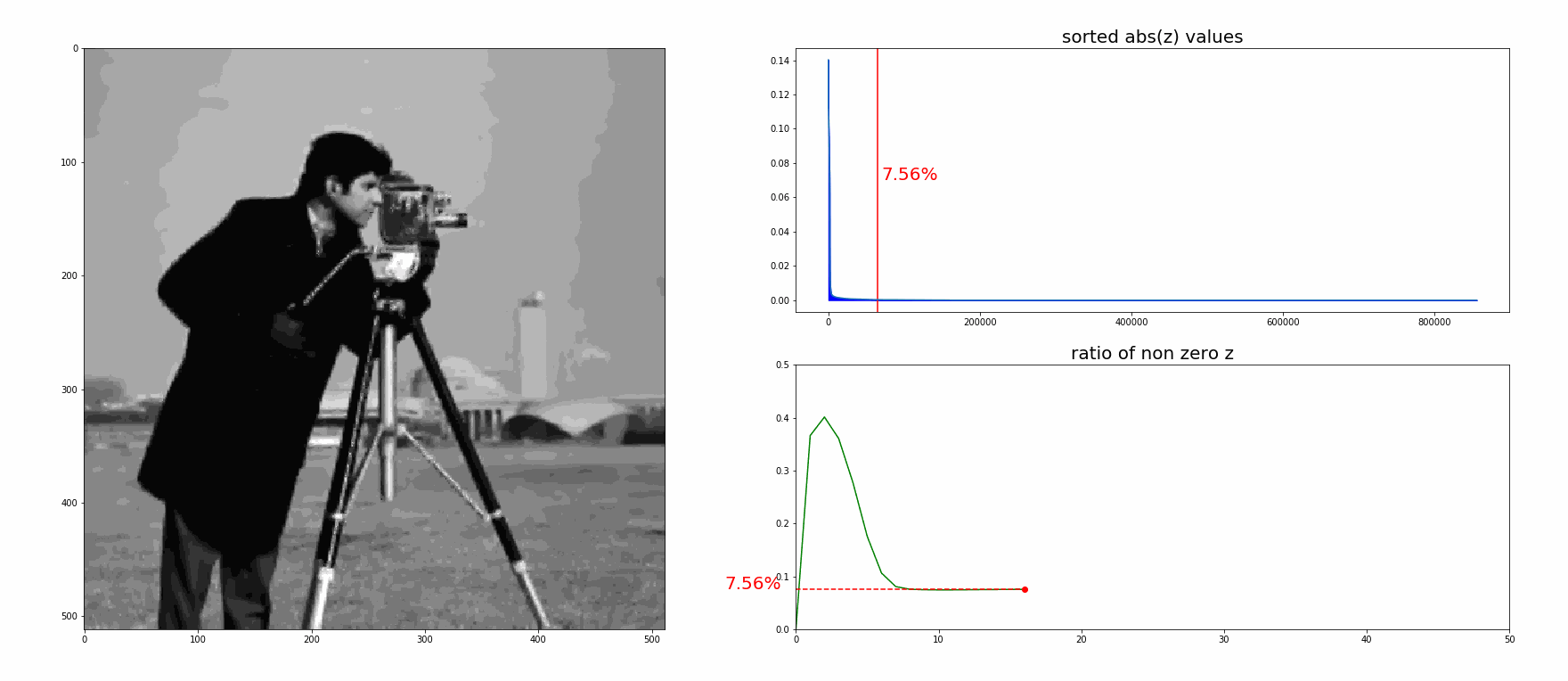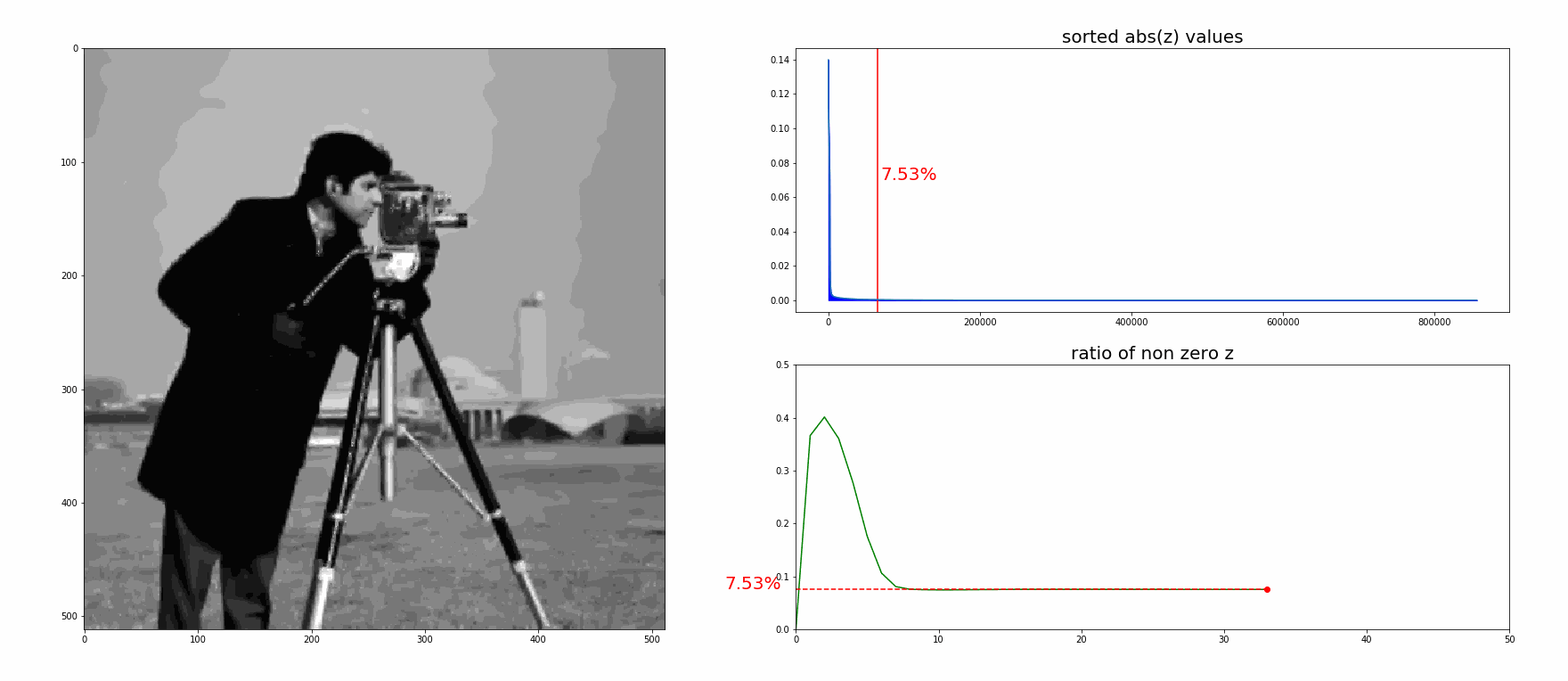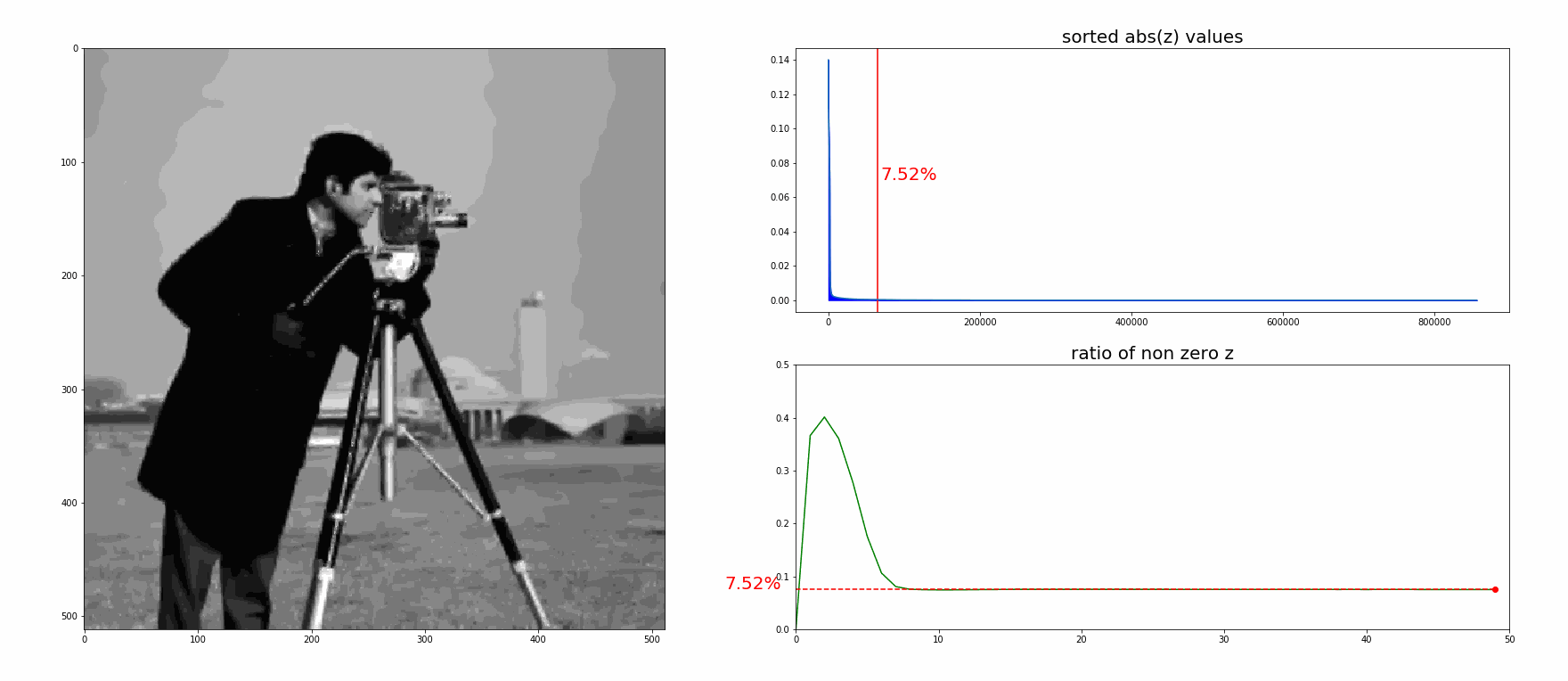
ADMMはこの拡張ラグランジュ関数を各変数に対して交互に更新していくことで元の最適化問題を解きます。 各変数の更新の式は\( \gamma = 1 / \rho , \ v = \gamma \lambda\)とすると
\[ \begin{aligned} \phi_{k+1} & = \argmin_\phi \left( \frac{1}{2} \| P\phi - \eta \|^2_2 + \frac{\rho}{2} \| G\phi - z_k + v_k \| \right) \\[2ex] z_{k+1} & = \rm{prox}_{\gamma}^{\ell_1} (G\phi_{k+1} + v_k) \\[2ex] v_{k+1} & = v_k + G\phi_{k+1} - z_{k+1} \end{aligned} \]
\[ \begin{aligned} \phi_{k+1} & = \\[2ex] \argmin_\phi & \left( \frac{1}{2} \| P\phi - \eta \|^2_2 + \frac{\rho}{2} \| G\phi - z_k + v_k \| \right) \\[2ex] z_{k+1} & = \rm{prox}_{\gamma}^{\ell_1} (G\phi_{k+1} + v_k) \\[2ex] v_{k+1} & = v_k + G\phi_{k+1} - z_{k+1} \end{aligned} \]
\[ \left( ただし \rm{prox}_{\gamma}^{\ell_1}(u) := \argmin_w\left( \frac{1}{2}\| u - w \|_2^2 + \gamma \| w \|_1 \right) \right) \]
\[ ただし \rm{prox}_{\gamma}^{\ell_1}(u) := \argmin_w\left( \frac{1}{2}\| u - w \|_2^2 + \gamma \| w \|_1 \right) \]
高速・省メモリな計算法
行列計算の回避
画像データに対して上記のアルゴリズムを適用するためにはもう一つ大きな問題があります。 \(\phi\)は画像を1次元ベクトルに変換したものであったので、もし画像のサイズが512×512ピクセルであれば\(\phi\)はサイズ262,144のベクトルになります。 したがってGは数十万×262,144という超巨大な行列になり、32bitのfloat型で保持すれば数百GBものサイズになり、通常のPCであればメモリ上に乗せることも不可能になってしまいます。
しかしながら、Gの正体はもともとはウェーブレット変換や全変動(差分フィルタ)を行列で表現したものでした。それら自体は行列を用いずにアルゴリズムとして実装することができ、ベクトル\(G\phi\)を直接的に求めることが可能です。 また1番目の\(\phi\)の更新の式は2次問題なので解析的に解くことが可能ですが、あえて最小化問題として扱い、例えば準ニュートン法や共役勾配法などを用いることでGそのものを扱わずに解くことができます。 このようにして現実的な計算資源の下で画像の圧縮センシングが可能になりました。
再構成の実例